Become A Wizard
This is the manual to the ZX85 computer, a project dedicated to
Steve Vickers, the author of the manual and the firmware for the ZX
Spectrum computer.
Contents
- Introduction
- Meet the Console
- The Basics of BASIC
- Guess the Number
- 2048
Introduction
Welcome to ZX85, a programmable general-purpose computer for introducing children
between the ages of 6 and 106 to the centuries-old tradition of wizardry.
One could also say "regular symbolic manipulations under a Turing-complete set of
rules" instead of "wizardry" and that would be certainly correct, but the latter
seems a more fitting expression for the art of creating functioning mechanisms of unlimited
complexity by merely describing them in a special language. Wizardry has been around for much longer
than computers, so while computer programming is certainly wizardry, there is more to it than
programming computers. A large part of mathematics and science is also wizardry and so is genetic
engineering and many other important human endeavors. While capable wizards are today among the most
sought-after specialists, mastering this art is its own reward, being one of the most stimulating
intellectual exercises.
In this book, the first uses of important terms are set in bold italic.
Usually, you will find the explanation of these terms somewhere around their first use. If not, you
can look them up elsewhere or ask someone who knows what they mean. Framed texts are either
notes, providing additional information typically relating the discussed topic to the
broader context of the world beyond the ZX85 or trivia, interesting facts related to
the discussed topic, often providing a historical perspective or challenges. The
first word in the frame, set in bold regular tells you which one that particular
frame is. Texts that you should see on the screen, such as keywords, program line numbers, listings,
reports and so on, are set in the native font of ZX85.
To be continued...
Meet the Console
The console is how wizards talk to
computers, in their own language. Unlike the
desktop, which is what muggles use to get the
computer do what they need, the console allows you, in principle, to
make the computer do anything that the computer is capable of
doing at all. It might seem less fancy, but it is far more powerful and
expressive than the desktop. Different computers might speak different
languages on their console, but they are, in many ways, similar.
The language your ZX85 understands is called BASIC,
which stands for
Beginner's
All-purpose
Symbolic
Instruction
Code.
There are many dialects of BASIC; ours is an evolution of ZX
BASIC, developed for Sinclair's ZX line of computers in the early
1980's. In particular, it is to a large extent backwards compatible with
that of the ZX Spectrum, upon which ZX85 is
based.
When you turn on your ZX85, it performs a quick self-test and greets
you with the following message near the bottom of the screen:
© 2019 ePoint Systems Ltd
© 1982 Sinclair Research Ltd
You are using the console now. It is, essentially a dialog with the
computer, similar to instant messaging. You type something, hit the
ENTER key and the computer responds. ENTER is just about the most
important key on the keyboard. Just pressing it means, "Okay computer,
I've typed in your orders. Now go and obey them."
As you start typing, you can immediately notice that the screen
is divided into two parts by a black stripe with a rainbow:
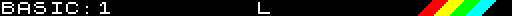
In fact, the part below the stripe is the console, the part
above it is the canvas. Inside the
stripe, you find the following information: BASIC stands
for the kind of input the console expects from you. In this case, it
expects a sequence of statements in BASIC. Then you have
:1, which just indicates that you are about to type the
first statement. Near the middle of the stripe, you see an
L character, which is the current input
mode. It tells you that if you press a letter key, it will
produce a lower-case letter (try it!). The
rest is just decoration.
The blinking square is the so-called cursor
which shows you where what you type is going to appear. If you have
already typed in anything, you can move the cursor using the arrow keys.
You can also delete what is before the cursor (which is normally what
you have typed last) by hitting the DELETE key.
If you press CAPS LOCK, the mode changes to C which
stands for capital-case letters (try!). You
can change back to L mode by hitting CAPS LOCK again. You
can also type capital-case letters in L mode by pressing
and holding the SHIFT key before hitting the letter key. The
SHIFT key needs to be pressed while you are hitting the letter key in
order for it to produce a capital letter. If you keep any key pressed
long enough, it will repeat its function. To type the symbols on either
number or letter keys, you should press the SYM key (also called
Symbol Shift) similarly to how you type
capital-case letters with SHIFT.
Note: On many other computers, the symbols
on number keys are typed with the SHIFT key, while the symbols on letter
keys are typed with some other shift-like key (typically ALT GR).
Not on a ZX! Here, all symbols are
consistently typed with Symbol Shift, while SHIFT'ed numbers are
performing the functions of control keys (for example, SHIFT+1 is the
same as EDIT, which will undo everything you have typed so far). Be
careful with those.
Now you know enough to start chatting with the ZX85.
The Basics of BASIC
If you try to greet the computer by typing Hello ZX! and
hitting ENTER, the cursor will jump to after the first letter. This is
the computer's tactful way of telling you it does not understand a word
you're saying. In fact, the cursor is moved to after the first character
that the computer did not understand; the very first one, in this case.
Any valid statement in ZX BASIC must begin with a so-called
instruction keyword. They are,
in alphabetical order, the following:
AND
BEEP
BORDER
BRIGHT
CAT
CIRCLE
CLEAR
CLIP
CLOSE #
CLS
CONTINUE
COPY
DATA
DEF FN
DELETE
DIM
|
DISPLAY
DRAW
ELSE
END IF
END PROC
END WHILE
ERASE
EXIT
FLASH
FOR
FORMAT
GO SUB
GO TO
IF
INK
INPUT
|
INVERSE
LET
LIST
LLIST
LOAD
LOCAL
LPRINT
MERGE
MOVE
NEW
NEXT
ON ERROR
OPEN #
OUT
OVER
PALETTE
|
PAPER
PAUSE
PLAY
PLOT
POKE
POP
PRINT
PROC
RANDOMIZE
READ
REM
RENUM
REPEAT
RESTORE
RETURN
RUN
|
SAVE
SCALE
STACK
STEP
STOP
UNTIL
USR
VERIFY
WHILE
WRITE #
YIELD
|
If you type Draw. and hit ENTER, you will notice that as
soon as you type the period, all the letters of the word
DRAW are turned to capitals, an extra space is inserted
before the period and the cursor is flashing after the period. The
computer does still not understand what this is supposed to mean, though
it understands a bit more than last time.
Note: Even though the keywords of BASIC are mostly
English words, BASIC is not English. For the computer to
understand what you type, it needs to be correct BASIC, not correct
English. For instance, in BASIC, you do not end statements with a
period.
If you move the cursor around, the computer won't let you move it
inside the (now capitalized) keyword anymore; it jumps from one side, to
the other. That is because it has recognized the keyword and now treats
it as a single unit, a so-called token.
Trivia: Statements instructing the
computer to answer us in writing begin with the PRINT
keyword. The reason for this is historical: computers got consoles
before they became able to display anything on screens. In those days,
the console's output was a roll of paper on which things were literally
PRINTed. While this has no longer been the case for many decades now,
the keyword stuck.
So let's try this: type PRINT 2+2 and hit ENTER. The
computer dutifully writes 4 on the canvas and reports
0 OK, 0:1
on the console. Note, that we get the same result no matter which letters
are capitalized in the PRINT keyword; pRiNt 2+2
would work just the same.
What happened here? The 4 is, as you might have guessed,
the evaluation of 2+2. OK means what
you'd think it means: that there was no error in executing this
statement. The 0:1 after the comma tells us that this was
the first statement (:1, same as in the black stripe) of a
sequence entered from the console. The very first 0 in the
report is the report code identifiying the report.
0 stands for OK. While we need to talk to the
ZX85 in BASIC, it reports to us in English. However, it can be changed
to report in other human languages as well, in which case the text of
the report might change to the point of unintelligibility for those who
do not know that particular language, but the report code remains the
same, no matter what the langauge of the report is. Thus, one can
understand what the report says even without understanding the language
in which the computer is reporting, given a full list of error codes. If
the computer needs to read its own or another computer's reports, it
can just look at the report code, ignoring the text in a language which
it does not understand (such as English).
So, now you can use the computer as a calculator. But if you type
PRINT Hello and hit ENTER, instead of a greeting on the
canvas, we get an error report:
2 Variable not found, 0:1
This is because Hello is treated as a
name of a variable
(more on this a bit later), not as a text to print. If we mean a
specific text, in BASIC, we must put it inside double quotes.
PRINT "Hello" actually does write
Hello on the canvas.
Note: Computers are very fussy that you should
distinguish between the digit zero and the letter O. To make it
absolutely clear, zero appears on the screen as 0, with a
slash through it. You also need to distinguish between the digit one
(1), the capital letter i (I) and the small
letter L (l). All ten digits are on the top row of the
keyboard. Furthermore, you must use the star (*) for
multiplication, not the letter x.
Instructions given on the console are called
commands. However, one can also assemble
sequences of instructions, which are called
programs and execute them together. Type
1 PRINT "Hello World!"
in the console and hit ENTER. Instead of just writing Hello
World! on the canvas, the entire command gets "moved" up
to the canvas. Something very important has happened: you have just written
your first computer program. Congratulations!
Trivia: ZX BASIC is a programming language in which
the instructions for programs and the instructions for commands are
exactly the same. Such languages are called scripting
languages, because programs are like scripted commands.
To run the program, just type the
RUN command. It does write Hello World! on the
canvas, just like in the previous example, but the report is slightly
different:
0 OK, 1:1
The difference is the statement identifier. It says 1:1
now instead of 0:1. This is because the last statement
executed was not directly from the console, but from program
line 1. You can enter another program line, too:
2 PRINT "My name is ZX85."
When you ENTER this program line, it also moves up and you see this in
the canvas area:
1 PRINT "Hello World!"
2>PRINT "My name is ZX85."
That little > sign after line number
2 is the so-called program
cursor. You can move it up and down with the arrow keys
and bring the pointed program line back down to the console by pressing
the EDIT key for further EDITing. Now try giving your ZX85 a personal
name by EDITing line 2. If you wish to delete a program line, just
enter its number without any instructions. Thus, for example, entering
1 would remove the greeting from before the
self-introduction.
In order to make it easier to insert new program lines in between
existing ones, there is a convention to number program lines by the
multiples of 10. The command RENUM re-numbers the program
to follow this convention. After RENUM. the two-line
program above becomes this:
10 PRINT "Hello World!"
20 PRINT "My name is ZX85."
Re-numbering does not change what the program does, at least for
well-written programs, it just makes it easier to work on it.
Now you know enough to start programming your ZX85. In each of the
following chapters, you find programs of increasingly complex computer
games and explanations of how and why they work. You are encouraged to
modify them, make them better and, eventually, write your own games
Guess the Number
The following ten-line program is a simple number guessing game. The
computer picks a random number between 1 and 1000 and you need to guess
it. After each guess, the computer would tell you whether your guess was
correct, too high or too low. Based on this information, you can close
in on the number picked by the computer. Type in the following program
and then enter the RUN command to play a game.
10 LET number=1+INT (1000*RND)
20 LET guesses=0
30 REPEAT
40 INPUT "Your guess?",guess
50 IF guess<number THEN PRINT guess;" is too low."
60 IF guess>number THEN PRINT guess;" is too high."
70 LET guesses+=1
80 UNTIL guess=number
90 PRINT "Congratulations, you guessed ";number;"."
100 PRINT "It took you ";guesses;" guesses."
When the game ends, the console shows the following report:
0 OK, 100:1
By now, you know what that means. You can always play another round by
entering RUN again.
Note: When the game asks you to guess a number, the
separator stripe between the canvas and the console says
NUMERIC instead of BASIC which means that it
expects a number or a numeric expression; a
formula that, when evaluated, results in a number. So, if you type
100+200, it qualifies as a guess of 300. Try
it!
Challenge: This behavior actually allows the player
to "cheat" and always guess the number picked by the computer
correctly upon first attempt. Wizards that are good at noticing and
exploiting such opportunities are called hackers.
Can you think like a hacker and win the game in one guess every time?
Now, let's see what it actually does. In the first two lines
(numbered 10 and 20, respectively), the
instruction keyword is LET. It
assigns values to
variable names. That is, it LETs the name mean
a particular number, until further assignments. For example, in line
20, the variable name guesses is made to stand
for zero. You can try it separately. If you enter that line without the
line number and then type PRINT guesses it will output
0. If you enter LET five=2+2 and then
PRINT five, it will output 4. This is
perfectly OK, because five is just a name, and
when a wizard uses a name, it means just what the wizard chooses it to
mean — neither more nor less.
Note: In ZX BASIC, anywhere where you can enter a
number, you can also enter numeric expressions. There is only one
exception from this rule: the line number before statements. Thus
2+2 PRINT is not correct BASIC, but anywhere else where
4 is accepted, 2+2 or 2*(1+1) is
also accepted and means the same.
Line 10 has two keywords that are not even on the list
of the previous chapter: INT and RND. This is
because they are not instruction keywords. BASIC statements cannot begin
with those. Let's explore them in more detail!
RND is similar to variables, except that it does
not need to be assigned and changes its value all by itself. It means a
random number that is at least zero and always less than 1. If you enter
PRINT RND, it will output a different fractional number
every time. Once in a while, it will output 0, though the
chances of that happening are pretty slim: one to 65536. It will never
output 1, though it can get pretty close.
Thus, 1000*RND is a number that is at least zero and
always less than 1000. Try PRINT 1000*RND a few times. Most
of these numbers have a fractional part after a decimal point. This is
what INT removes. INT is a
function that does something to the number
that follows it. In particular, it turns it into an
integer (which is just wizard-speak for whole
numbers), removing the fractional part of numbers greater than zero.
However, PRINT INT 1000*RND does exactly the same as
PRINT 1000*RND (try!). This is because the number that
follows INT is 1000 so it takes the whole part
of 1000, which is still 1000. Only then is it multiplied by
RND. Similarly, INT RND * 1000 is still not
what we want (try it!), because the number following INT in
this case is RND. Since RND has only a
fractional part, INT RND is always zero. If you multiply
that by 1000, it is still zero.
To exactly determine the order of operations, you need to use
( and ), the so-called
parentheses. What is between these is
evaluated before what is outside of them. Hence, INT
(1000*RND). This results in a random whole number that is at
least zero and less than 1000, that is at most 999. But since we want a
random number between 1 and 1000, 1 needs to be added to it. Actually,
INT (RND*1000)+1 would work just the same. This is because
the results of multiplication and addition do not change if we switch
the order of the numbers to multiply or to add. Wizards call such
operations commutative.
Line 30 contains a single keyword REPEAT.
It means that what follows until the keyword UNTIL (see
line 80) must be repeated. It must be repeated
UNTIL the condition following that keyword becomes true.
In our case, until the player's guess and the number
picked by the computer (in line 10) become equal.
Now let's look to the four lines between REPEAT and
UNTIL, which is what needs to be REPEATed.
Line 40 begins with the keyword INPUT. Its
purpose is somewhat similar to that of LET in that it
assigns values to variables, but, unlike LET, it reads the
value from the console. The keyword INPUT is followed by a
list consisting of things to write to the console and variable names
which are to be assigned the values read from the console. These can be
separated by comma (,, SYM+N), semicolon (;,
SYM+O), or apostrophe (', SYM+7). The difference is where
the next item is going to appear on the console: in case of a comma, it
is going to be neatly tabulated to either the middle of the line, or, if
there is no space for that, to the beginning of the next line, in case
of a semicolon, it is going to appear right after the end of the
previous item, while in case of an apostrophe, it is going to appear at
the beginning of the next line. Try changing the separator between
"Your guess?" and guess in line
40 to see all this in action.
Lines 50 and 60 begin with an
IF keyword followed by a condition, a THEN
keyword and a PRINT statement. Such program lines execute
the part after THEN only IF the condition following
IF holds true.
Line 70 contains an unusual LET statement,
a so-called update. It is, essentially, a
shorthand for LET guesses=guesses+1. It requires less
typing on the wizard's part and less interpreting on the computer's
part.
Line 80 closes the loop
started in line 30. It is called a loop, because if you
draw little arrows from each statement to possible next statements, your
arrows are going to form a loop; a sequence of statements to be
(possibly) repeated.
Trivia: Loops that read the console and depending on
what has been entered print something are called REPL by
wizards, which stands for
Read -
Evaluate -
Print -
Loop. If you think about it, ZX BASIC itself is a REPL.
Lines 90 and 100 are just regular
PRINT statements. Just like in INPUT the
separators between things to be printed determine how they are going to be
positioned relative to one another on the canvas.
How many attempts do you need to guess the number without cheating?
Let's switch sides with the ZX85 now and write a program that plays this
same game as the guesser: the player thinks of a number and the computer
tries to guess it.
10 PRINT "Think of a whole number between 1 and 1000."''
20 LET low=0: LET high=1024
30 REPEAT
40 LET guess=(low+high)/2
50 PRINT "Is it ";guess;"?",
60 INPUT "0: Too high."'"1: Too low."'"2: Correct."'answer
70 IF answer=0
80 LET high=guess
90 PRINT "0: Too high."
100 ELSE IF answer=1
110 LET low=guess
120 PRINT "1: Too high."
130 ELSE IF answer=2
140 PRINT "2: It is ";guess;"."
150 STOP
160 ELSE
170 PRINT "I do not understand ";answer;"."
180 END IF
190 UNTIL high-low<2
200 PRINT "This cannot be."'low;" is too low, but ";high;" is too high."
You may have noted that the initial high number is 1024, rather than 1001.
The reason for this is to make sure that the division in line 40
always results in a whole number, since
1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
that is two multiplied by itself ten times or, as wizards say:
"two to the power of ten". It is written like 210.
Thus, 1024 can be divided by 2 ten times, which is, not entirely by lucky
coincidence, the maximum number of guesses the computer needs to guess a
whole number between 1 and 1000.
The operation of multiplying a number by itself (or taking
powers in wizard-speak) is denoted by the upwards-pointing arrow
(^, SYM+H) in ZX BASIC. Try PRINT 2^10.
Play this game a few times and note the sequences of answers you give
to ZX85. It will always guess the number in no more than 10 questions and
for any given number, the sequence of questions and answers will be the
same. In fact, if you know that the number is somewhere between 1 and 1000,
the answers you give already uniquely identify the number. Now let us
modify the game a little bit. Change the following lines:
50 PRINT "Is it at least ";guess;"?";TAB 22;
60 INPUT "0: No, it is not."'"1: Yes, it is."'answer
90 PRINT "0: No."
120 PRINT "1: Yes."
200 PRINT "The number is ";low;"."
Then delete lines 130 through 150. You can
accomplish this by the command DELETE 130 TO 150. The new
keyword TAB in line 50 is similar to the
comma, but it can tabulate to any position (22, in our case), not just
the middle of the line, which would be TAB 16.
Now you can RUN this "new game". It is now more
similar to Twenty Questions in that every question is answered
by either "yes" or "no". However, the computer will
always guess the number in exactly 10 questions. For example, 500 would be
guessed like this:
Is it at least 512? 0: No.
Is it at least 256? 1: Yes.
Is it at least 384? 1: Yes.
Is it at least 448? 1: Yes.
Is it at least 480? 1: Yes.
Is it at least 496? 1: Yes.
Is it at least 504? 0: No.
Is it at least 500? 1: Yes.
Is it at least 502? 0: No.
Is it at least 501? 0: No.
The number is 500.
If you change
the 1000 in line 10 to 1000000
(one million) and also high in line 20
from 1024 to 2^20 it will ask 20 questions before
guessing the number. Any integer up to a million in just 20 yes/no
questions!
Trivia: The strategy of picking the middle element
in some ordering, comparing it to what you are looking for and based on
whether or not it is greater, continuing either with the lower or the
upper half of the ordering is called binary
search and it is the wizard's way of quickly finding
needles in haystacks. It is a simple, yet very powerful strategy (or
algorithm in wizard-speak) from a broader
class of divide and conquer algorithms. You
are going to learn many of those and maybe invent some of your own.
Our word "algorithm" is honoring an outstanding medieval wizard,
Muhammad al-Khwarizmi, who invented or rigorously described several
algorithms that we regulary use to this day.
The answers in this game do uniquely identify the
integer and you do not even need to know how large it can be, as that
can be learned from the number of answers. It is called
binary representation and this is how
computers represent numbers internally. In ZX Basic, you can use this
representation using the BIN keyword. For example, you can
write BIN 0111110100 instead of 500. Moreover,
you can omit the leading zeroes, so BIN 111110100 also
means 500.
In general, everything is a sequence of zeroes
and ones for the computer. Just like in the game above, it is common
practice to represent "yes" by 1 and
"no" by 0. ZX85 actually does it all the time.
For example, ask it whether two is less than one by typing PRINT
2<1. It will answer 0 by which it means
"No.". But to PRINT 2>1 or to
PRINT 2+2=4 it will answer 1 by which it means
"Yes.". Anywhere where you can write answers to yes/no questions,
you can also write numeric expressions, where those evaluating to zero
will be taken as a "no", everything else as a "yes".
For example, IF 0 THEN PRINT "zero" will not output anything,
but IF 1 THEN PRINT "one" will output one to
the canvas, and so will IF 5 THEN PRINT "one".
Binary numbers are very important in wizardry, or as wizards call it,
computer science. Those wishing to become
wizards better learn to use them as second nature. For example, you
should get into the habit of counting on your fingers in binary. Thus,
instead of just 5, you will be able to count up to 31 on the fingers of
one hand (be careful with showing number 4 to other people; muggles
might misunderstand you). Each digit (which is
just Latin for "finger") in a binary number corresponds to a
power of 2. Your thumb corresponds to 1 (which is 20), your
index finger corresponds to 2 (21), your middle finger to 4
(22), your ring finger to 8 (23) and your pinky to
16 (24). For example, if you want to show 7, you only extend
your thumb, your index finger and your middle finger, becase 1 + 2 + 4 =
7 (try PRINT BIN 00111). An extended thumb, index finger
and pinky means 19 (which is 1 + 2 + 16, BIN 10011). In
general, if you want to find out the binary representation of a number,
you can either play the game above, or use another keyword,
STR$. For example, PRINT STR$ (30,2) will be
answered with 11110 (try it!), meaning all except your
thumb extended. STR$ is used to obtain various
representations of numbers, with 2 meaning binary. The
parentheses are needed, because otherwise STR$ will only
concern itself with 30, the comma would mean tabulation to
the middle of the line and 2 would mean 2. Try!
Trivia: While all actual computers used today by
humans are binary, it is not the only reasonable choice for digital
computers. The reason humanity ended up using binary computers
exclusively is that there are tremendous benefits in all computers being
based on the same logic so that many things only need to be done once
and used everywhere. The other reasonable choice for digital computers
is ternary, which is based around the powers of 3 rather than
two. The three kinds of digits there are -1, 0 and +1, meaning
"no", "unknown" and "yes". Alien computers
may very well be ternary. In fact, humanity has also explored ternary
computing, an effort culminating in the serial production of a ternary
computer named Setun' after a creek flowing through the campus of
Lomonosov University in Moscow, Russia. But by the time the details were
worked out to the point of practicality, binary computers were so
widespread that it did not make much sense to continue.
However, this choice does not matter all that much. All digital
computers can "pretend to be" (wizards say
emulate) any other digital computer, so the
(amazingly broad and to this day largely unexplored) set of problems
that can be solved by digital computers does not depend on this choice.
This universality (called Turing-completeness
in his honor) was discovered and proven by an outstanding British wizard
in the middle of the twentieth century, a pioneer of electronic
computing, Alan Turing.
2048
Now is the time to write the first game that is actually a lot of fun
to play, to the point of being mildly addictive. The author readily
admits to spending most of a twelve-hour trans-pacific flight playing
this game on the onboard entertainment system. Playing this game will
also help you memorize the powers of two. This game called
2048 was designed by an Italian wizard, Gabriele
Cirulli in 2014.
The game is played on a 4×4 grid, starting out empty. Every turn, a
new tile with a value 2 or 4 will appear in one of the empty spots. The
player can slide the tiles with the arrow keys. Each tile slides until
it hits another tile or the edge of the grid. When two tiles with the same
number collide, they will merge into a tile carrying their total value.
The resulting tile will not merge in the same move. The game is won when
a tile with a value of 2048 appears. We can clear the board and restart
the game any time pressing the DELETE key.
We will add score- and time-keeping, colorful graphics and music to
our game later, first we write the most important parts of the game so
that it can be played. Let's begin with drawing the grid:
10 LET b$="+----"*4+"+"+CHR$ 13
20 PRINT (b$+("| "*4+"|"+CHR$ 13)*4)*4+b$
There are several new things here. The variable name b$
ends with $ pronounced as string,
making b$ a string variable. The
value it holds is a string, rather than a number. Strings are sequences
of characters, which can be letters, digits,
symbols, tokens or control
characters. In fact, the quoted texts in previous examples
are all strings. In the assignment of b$ in line
10, there is a string expression. The
+ between two strings results in a new string, consisting
of the lefthand string immediately followed by the righthand string. For
example "Hello"+"World!" would result in
HelloWorld!. Try it! If there is a * between a
string and a number (or a string expression and a numeric expression),
it repeats the lefthand string the righthand number of times. For
example, "!"*3 results in !!!.
There is also a new keyword, CHR$. Keywords ending with
$ are string valued functions
that turn their arguments into strings. In particular CHR$
turns the number following it into one character with that particular
character code, if that number is between 0 and 255. Character
codes between 0 and 23 are control characters.
Among them, CHR$ 13 is known under a number of names:
Carriage Return, CR, Enter, New Line, Return, but they all mean
the same thing. It indicates the end of a line and a beginnig of a new
line.
Thus, line 10 assings the following string to b$:
+----+----+----+----+
You can verify this by entering PRINT b$.
Note: The program would work exactly the same, if we
changed line 10 to this:
10 LET b$="+----+----+----+----+"+CHR$ 13
However, that would take more time to type and would take up more memory of the
computer. By typing a long and repetitive line like that the wizard does
something that a computer can do better and faster. Why not let the computer
do all this tedious work?
Line 20 uses b$ to draw the grid using similar
techniques. By now, you know enough to understand every detail of it. Of
course, instead of those two lines, one could naively write a sequence of
PRINT statements:
1 PRINT "+----+----+----+----+"
2 PRINT "| | | | |"
3 PRINT "| | | | |"
4 PRINT "| | | | |"
5 PRINT "| | | | |"
6 PRINT "+----+----+----+----+"
7 PRINT "| | | | |"
8 PRINT "| | | | |"
9 PRINT "| | | | |"
10 PRINT "| | | | |"
11 PRINT "+----+----+----+----+"
12 PRINT "| | | | |"
13 PRINT "| | | | |"
14 PRINT "| | | | |"
15 PRINT "| | | | |"
16 PRINT "+----+----+----+----+"
17 PRINT "| | | | |"
18 PRINT "| | | | |"
19 PRINT "| | | | |"
20 PRINT "| | | | |"
21 PRINT "+----+----+----+----+"
But typing all that would be a huge waste of the wizard's time and the
computer's memory. There are computer programs having such repetitive
patterns in them and there are legitimate justifications for writing
software like this, but these are typically written by another computer
program. In a later chapter, we shall see how to write computer programs
writing computer programs.
30 DIM b(4,4)
The DIM keyword allocates an
array. In this case, b is a
numeric array, a collection of numeric
variables. The numbers between parentheses following the array's name
are called dimensions. Each element in the
array is a variable that can be assigned a value. Initially, all of them
are zero. One way to think about DIM is that it creates as
many variables as the product (which is just
wizard-speak for multiplication) of all its dimensions, in our case 16.
Each variable's name is the name of the array, followed by a list of
subscripts in parentheses, separated by
commas. Each subscript is a number between 1 and the corresponding
dimension. So, for example, b(3,2) is one of these
variables, but b(1,1,1) or b(5,2) are not, if
b was allocated according to line 30. Try it!
If you use wrong subscripts, ZX85 will report
3 Subscript wrong, an error.
The benefit of arrays compared to just naming variables, say,
b11 or b32 is that subscripts can be numeric
expressions. That is the choice of which one to access or assign can
depend on other variables. A typical example when arrays are useful is when
the same operation needs to be performed with many variables. Without arrays,
one needs to write out the same operation for every variable. This is tedious
work not worth a wizard's time. Instead, you can (and should) use an array
and write a loop and make the computer perform the same operation on various
elements in the array. The wizard only needs to spell it out once. You will
see many examples of this in the game.
After drawing the board on the screen and allocating it in the
computer's memory (as array b will hold the
state of the board). we are ready to write the
main loop of the game. Just like in the
previous number guessing games, the main loop describes what happens in
each turn of the game. Unlike the previous games, the main loop here is
not a REPL, as the game only uses the canvas, not the console.
40 REPEAT
50 PROC drop()
60 REPEAT
70 LET action=0
80 REPEAT
90 LET k=CODE INKEY$
100 UNTIL k>=8 AND k<=12
110 IF k=8 THEN PROC tilt(1,1,0,1)
120 ELSE IF k=9 THEN PROC tilt(4,4,0,-1)
130 ELSE IF k=10 THEN PROC tilt(4,1,-1,0)
140 ELSE IF k=11 THEN PROC tilt(1,4,1,0)
150 UNTIL action OR k=12
160 PROC board()
170 UNTIL k=12
180 RUN
In line 50, there is a new and very important keyword:
PROC. It calls (or invokes) a
procedure. A procedure is a program that has a name and can be
executed from another program (or itself). In this case, the name is
drop and the empty parentheses after the name indicate
that it has no parameters. As its name might suggest, it drops a
tile with 2 or 4 on it onto a random empty cell of the grid. How
it does it is described later in the program.
The most important role of procedures is that it allows the wizard
not to write the same sequence of statements in multiple places in the
program. As you might have noticed, this kind of laziness is a cherished
trait of wizards.
But drop is not called from anywhere else in our game.
In line 50 we use a procedure for a different purpose. It
has to do with making the code more understandable for other wizards,
which very much includes ourselves some time later. A wise wizard
acknowledges and works around the limitations of the human mind,
including ones own. One such limitation is that we have a difficulty
thinking on different levels of detail at the same time and even more
difficulty following someone else's thoughts if they are doing that. It
is important to keep in mind that even a mere two weeks from now you
will be a different person. A very typical source of frustration with
poor wizardry is trying to understand our own code written a long time
ago. In the main loop of our game, we spell out the rules of the game
and should not get into the minute details of placing a tile at a random
empty location. There are no strict rules about what parts of code to
place in separate procedures; it is an art, mastered with practice.
However, if you find that it took you too much effort understading part
of a program because it worked on a lower level of detail than
its surrounding, do not hesitate to move it out into a procedure and
give it a name that describes what it does, not getting into
the details of how it is done. Such re-arranging of the code is
called refactoring and even though it takes
some effort, it saves a lot of time and nerves down the road. Avoiding
it is the wrong kind of laziness.
The loop between lines 60 and 150 keeps
running until something actually happens on the board. This is captured
in the variable action assigned in line 70
meaning no action and perhaps changed in one of the
moves in lines 110 through 140.
This is a loop within a loop, or as wizards call it, a
nested loop.
In turn, it has another loop nested in it between lines
80 and 100. In its
body, it has a single LET
statement with two new keywords. CODE is the reverse of
CHR$. It takes a string and, if it is a single character,
turns it into its character code, which is a number. The
CODE of an empty string is zero.
Try PRINT CODE "". The keyword
INKEY$ means the key pressed, or an empty string, if no key
is pressed. As the $ at its end suggests, it is a string.
Together, CODE INKEY$ means the character code of the key
that is pressed, or zero if there is none. You can try REPEAT:
PRINT AT 0,0;CODE INKEY$,:UNTIL 0 to see what code corresponds to
which key on the keyboard. Character codes 8 through 11 correspond to
the arrow keys, code 12 corresponds to DELETE. Hence, line
100 repeats the loop UNTIL one of them is
pressed. If it is DELETE, the outer loops also quit.
Lines 110 through 140 are there to
move the tiles in the direction of the arrow key pressed.
Note: If you felt a bit of tedium while typing them in,
it is a good sign, as this is somewhat unwizardly code, worthy of
refactoring. It works correctly, but the parameters of move
have to do with how to move the tiles in different directions,
even though at this level we are supposed to be thinking about
what needs to be done, not preoccupied with the minute details
of how. So let's refactor it! These four lines express that the
tiles need to be moved in the direction determined by the key pressed.
We can replace it with a statement that expresses it more clearly:
DELETE 110 TO 140
110 IF k<>12 THEN PROC tilt(k-8)
The <> sign means not
equal. This change will require further changes in the
definition of PROC move beginning
with line 310, which are discussed below it.
Line 160 redraws the board with all the tiles moved. The
reason why redrawing is not part of PROC move is that we
only want to redraw the board if some tiles have actually moved. Since the
loop above this line keeps repeating until it happens, at this point we
can be certain that at least one tile moved. The main loop continues until
the DELETE key is pressed, at which point the entire program is
RUN again.
Now it is time to flesh out the procedures called from the main loop. The
definitions of procedures begin with the @ label marker,
followed by the name of the procedure and its parameters. The definition
ends with the END PROC keyword.
190 @drop()
200 LOCAL x,y,k
210 FOR i=1 TO 4: FOR j=1 TO 4
220 IF NOT b(i,j)
230 LET k+=1
240 IF RND<1/k THEN LET x=i: LET y=j
250 END IF
260 NEXT : NEXT
270 LET k=1+(RND<.5)
280 LET b(x,y)=k
290 PROC tile(x,y,k)
300 END PROC
The drop procedure has no parameters. In line
200 we declare local variables.
These variable names are used by the procedure but we do not want the
procedure to interfere with the rest of the program, if it happens to
use the same variable names for different purposes. For example, in the
main loop we use k for the code of the key pressed, but
inside drop we use it as a counter of empty cells in the
grid and as the random value of the tile dropped. It is always a good
idea to declare every variable that we intend
to use inside a procedure as LOCAL, as it will reduce the
possibility of unintended side effects of
our procedure. Also, since local variables are considered first when
looking up a variable by name, this practice actually speeds up
the execution of our programs. Unless stated otherwise in the declaration,
local numeric variables are initialized to zero and local string variables
to the empty string.
Lines 210 through 260 describe two
nested FOR loops. These are loops that need to be executed
a given number of times (4, in our case). The FOR keyword
is followed by the name of the loop variable,
that is going to take a different value during each execution (or
iteration) of the loop. These values are
determined by what follows the = sign: 1 TO 4
means that it will be first assigned 1, then 2 and so on until the last
iteration in which it will be assigned 4. Thus, variables i
and j will be assigned all 16 possible combinations.
Try FOR i=1 TO 4:FOR j=1 TO 4:PRINT "i=";i,"j=";j:NEXT:NEXT
to get a better understanding of what goes on here.
Note: The loop variable is always local to the loop.
The following command prints numbers from 1 to 5:
FOR i=1 TO 5: PRINT i: NEXT
Afterwards, however, PRINT i results in a
2 Variable not found, 0:1
report, because
i is accessible only inside the loop.
There are no side effects even when nesting two loops with the same
loop variable name. Try this:
FOR i=1 TO 10: FOR i=1 TO 10: PRINT "*";: NEXT: PRINT: NEXT
It will output a grid of 100 stars to the console:
**********
**********
**********
**********
**********
**********
**********
**********
**********
**********
Lines 220 and 250 mean that the entire body
of these two nested loops is conditioned on b(i,j) being
empty. An IF statement without a THEN keyword
after the condition continues with the next statement, if the condition
is true. If it is false, absent of an ELSE keyword,
it continues after the matching END IF keyword. In this case,
lines 230 and 240 are only executed if
NOT b(i,j) in line 220 is true, that is
if b(i,j) equals zero. This also shows the power of arrays,
as we can test 16 variables in a single loop with a handful of statements.
Line 230 counts empty cells in the grid in variable
k. Line 240 replaces the values of
x and y with the current values of
i and j if with a probability
1/k. In other words, at random, on average 1 out of
k times, those values are replaced. At the first empty
cell, when k=1, they are replaced with certainty, as
RND is always less than one. When the loops have run their
course, x and y contain the subscripts of one
of the empty cells chosen randomly and uniformly from among all the empty
cells.
At this point, k contains the number of empty cells, but
we do not want to do anything with that number. So, in line
270 we reuse k for a different purpose: it
becomes either 1 or 2 with equal probability. It means which power of
two the new tile will be: 21 (2) or 22 (4). In
lines 280 and 290 this value is used to assign
the corresponding element of array
b and display the corresponding tile on the canvas.
PROC tile is defined later, beginning with line
580, as the details of drawing clearly do not belong to
the procedure of random placement of a new tile.
310 @tilt(i,j,x,y)
320 FOR n=1 TO 4
330 PROC slide(i,j,x,y)
340 LET i+=y: LET j-=x
350 NEXT
360 END PROC
The procedure move takes four parameters: the subscripts
of one corner of the board and the numbers by which they are changed in
each of the four iterations, as tile sliding and merging is calculated
for all four rows or columns. The local
variables to which parameter values are assigned are listed in the
parentheses after the procedure name in the DEF PROC
statement. How tile sliding is done is defined in procedure
slide, which is called in line 330. Since
parameter variables are local to the procedure, there are no side
effects from updating i and j in line
340.
Note: As noted in the discussion of the main loop,
it is better if the job of setting parameters i, j,
x and y depending on the direction of movement
would be the job of procedure move rather than the main loop.
The corresponding refactoring of procedure move would be
as follows:
310 @tilt(k)
315 LOCAL i=k?(1,4,4,1),j=k?(1,4,1,4),x=k?(0,0,-1,1),y=k?(1,-1,0,0)
Thus, PROC move takes a single parameter, the direction of
the movement, a number between 0 and 3. In line
315 the former parameters are declared as local variables
and initialized with the appropriate values. The question mark ?
operator is called selector and it picks
the corresponding value from the list in the following parentheses. In order
to be able to use conditions before the question mark, the first value is 0.
For any value greater than the number of expressions in parentheses, the
last one is used, though this can never happen in this program.
370 @slide(i,j,x,y)
380 LOCAL k=i,l=j
390 FOR n=1 TO 3
400 LET i+=x: LET j+=y
410 IF b(i,j)
420 WHILE b(k,l) AND b(k,l)<>b(i,j)
430 LET k+=x: LET l+=y
440 END WHILE
450 IF NOT b(k,l)
460 LET b(k,l)=b(i,j)
470 LET b(i,j)=0
480 LET action=1
490 ELSE IF b(k,l)=b(i,j) AND (i<>k OR j<>l)
500 LET b(k,l)+=1
510 LET k+=x: LET l+=y
520 LET b(i,j)=0
530 LET action=1
540 END IF
550 END IF
560 NEXT
570 END PROC
The parameters of procedure slide are subscripts
i and j of the first cell of the row or column,
the one toward which tiles are going to slide. Parameters
x and y are the values that need to be added to
i and j, respectively, to point to the next
cell of the grid (array b).
The procedure also has a new type of loop in it, the WHILE
loop between lines 420 and 440. The condition
following WHILE is evaluated before each iteration
of the loop. If it is false (that is zero), then execution
continues after the END WHILE statement.
Otherwise, the body of the loop is executed and the condition checked
again.
Note: Both WHILE/END WHILE
and REPEAT/UNTIL loops depend on a condition.
The main difference is that REPEAT/UNTIL loops
execute at least once. WHILE loops are not
executed at all, if their condition is false in the beginning.
Another difference is that the condition after WHILE must
be non-zero but the condition after UNTIL must be zero for
the loop's body to be executed one more time.
But there is also a subtler difference. The condition after
WHILE is evaluated in the enclosing
context, meaning that variables local to the loop are not
accessible there. By contrast, the condition after UNTIL is
evaluated in the local context of the loop
itself, allowing for using variables local to the loop.
580 @board()
590 FOR i=1 TO 4: FOR j=1 TO 4
600 PROC tile(i,j,b(i,j))
610 NEXT : NEXT
620 END PROC
The board procedure simply iterates through all the cells of
the board and calls PROC tile to draw the tiles and empty
cells, as the case might be.
630 @tile(x,y,k)
640 LOCAL k$=k?("",STR$ (2^k))
650 LET k$=" "*(4-LEN k$)+k$
660 PRINT AT x*5-2,y*5-4;k$
670 END PROC
This last procedure is used to draw one empty cell or a tile corresponding
to subscripts x and y. The keyword LEN
means the length of the string after it. Line 650 makes sure
that k$ is always exactly 4 characters, with the number on the
tile at the end of the string.
When we are going to change the graphics of the game to look prettier,
have colors and so on, most changes go into this procedure. This first version
is very rudimentary, but it is (barely) enough to make the game playable.


